Heaps

A heap is an important data structure used for any operations involving prioritization. Examples include accessing or removing the largest or smallest priority object. Heaps will also support the insertion of new objects into the heap which maintain their behavior.
Learning Objectives
- Implement a traditional array-based MinHeap
- Implement a pointer-based MinHeap
- Explore and implement a basic one layer Bucket-Heap
- Begin to think about design decisions and trade-offs
Github Classroom
You can clone the starter files for this lab at this GitHub Classroom link. Be sure to open the assignment in VSCode and setup up your virtual environment following these instructions.
Implementation
Heaps are commonly implemented as a binary tree, as you have seen in CSCI 0200. In this lab, you will first implement an array based heap, where the tree is embedded in an array. Below is an image of a heap and how a heap is stored within an array.
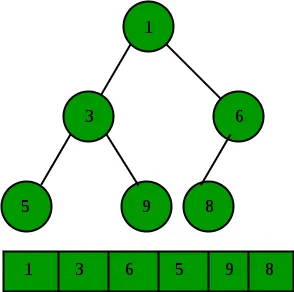
MinHeap
In this lab you are going to implement a MinHeap, where the element at the root (index 0) has the lowest priority. Our implementation of MinHeap will store PriorityItems, which have an integer priority and an associated value of any type. This means that the smallest priority within the heap at any time will be at the root.
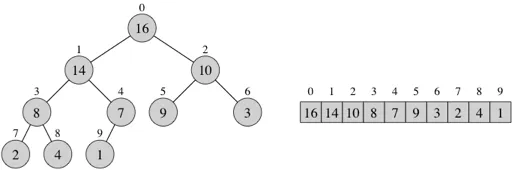
Note that the above example is a max-heap, but the array embedding is similar for the min-heap that you will implement in this lab.
Task: Fill out the stencil code to complete the first few functions in array_heap.py:
empty(): ReturnsTrueorFalsedepending on whether the heap is empty or notswap(): Swaps two nodes in the heap given their indicesget_left_child(): Gets the index of the left child of a node given its indexget_right_child(): Gets the index of the right child of a node given its indexis_leaf(): ReturnsTrueif the node is a leafget_parent(): Gets the index of the parent of a node if it exists
Checkout the docstrings for more details.
Now that we can build the heap and index elements within the heap, we need to work on supporting functions that help us maintain heap property.
Task: Implement the following heap functions in array_heap.py:
sift_up(): Called to move a node up to its correct position in the heap after insertionsift_down(): Called to sink a node down to its correct position in the heap
Hint: The following pseudocode may help:
function sift_up(node):
if node is root:
return
if node is greater than its parent:
swap node with its parent
recursively call sift_up on the parent
function sift_down(node):
if node is a leaf:
return
if node is greater than at least one of its children:
swap node with its smallest child
recursively call sift_down on the childTask: Implement the following core heap functions:
insert(): inserts an element onto the heap.extract_min(): Removes the element with the lowest priority from the heap. Returns this element and maintains heap property.peek(): Returns the minimal priority element in the heap.
Self Checkpoint: Run the tests in test_heap.py to ensure that your implementation is correct.
Note: This also includes tests for the PointerHeap, so you can ignore those for now.
ArrayHeap tests in test_heap.py pass!Pointer-Based Heaps
A heap can also be represented as a binary tree where each element is a node, and has access to its parent and children.
Task: Check out the Node class in pointer_heap.py. This class will be used to represent the nodes in the heap.
The pseudocode for most heap operations remain the same from the ArrayHeap, but now we need to be able to find the last node in the heap.
To do this, we can look at the binary representation of the current length of the heap, and use this to tree-walk to the last node added,
which will become the root when we extract a node off the heap.
We can do this in the code using the find_last_node_at_index method of PointerHeap.
Task: Implement the find_last_node_at_index method in pointer_heap.py.
The below pseudocode should help with find_last_node_at_index():
function find_last_node_at_index(index):
let b = binary representation of index (number of nodes)
Remove the most significant bit of b
Start at the root node
for each bit in b:
if bit is 0:
go to the left child
else:
go to the right child
return the node you end up at after traversalTask: Implement the sift_up and sift_down methods in pointer_heap.py.
These should follow a very similar structure to your implementations in array_heap.py, but with pointer semantics.
Task: Implement the insert, extract_min, and peek methods in pointer_heap.py.
These should also follow a very similar structure to your implementations in array_heap.py, but with pointer semantics.
Self Checkpoint: Run the tests in test_heap.py to ensure that your implementation is correct.
Note that now all of the tests in test_heap.py should pass, including the tests for the PointerHeap.
TA Checkpoint: Show a TA that all of the tests in test_heap.py pass!
Additional Info
Heaps / PriorityQueues in Python are contained in a built-in module in Python! Its documentation can be found here for future use so you don’t have to reimplement heaps yourself.
Bucket Heaps (Optional)
So far we have implemented the traditional MinHeap two different ways.
Similar to different types of sorting like BucketSort/RadixSort, in certain cases we can achieve better performance by straying from conventional Heap mechanisms if we know something about our input.
Within this next part, we will implement a Bucket MinHeap which is a data structure where we restrict insertions to the heap to be monotonically increasing. You will further explore the uses of bucket-heaps later during Djikstra’s algorithm.
Consider the basic idea of a bucket heap:
- Creates buckets where is the maximum “priority”.
- Maintain a current bucket variable, which will only increase towards higher priority buckets. Since by assumption inserts are monotonic, we never need to search previous buckets.
- Inserting adds the item to the bucket corresponding to its priority.
- Extracting and peeking first updates the current bucket to find the first non-empty bucket before performing its usual function.
Task: Implement the insert, extract_min, and peek methods of BucketHeap in bucket_heap.py!
Self Checkpoint: Run the tests in test_bucket_heap.py to ensure that your implementation is correct.
Final Checkpoint: Show a TA that all of the tests in test_bucket_heap.py pass!